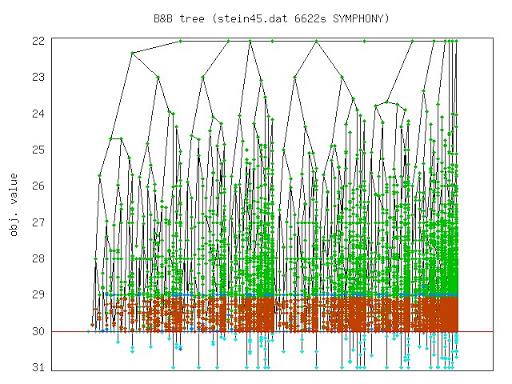
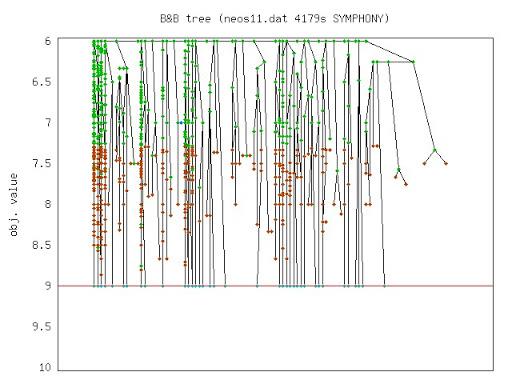
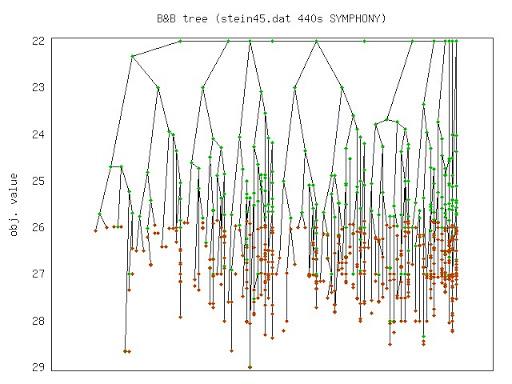
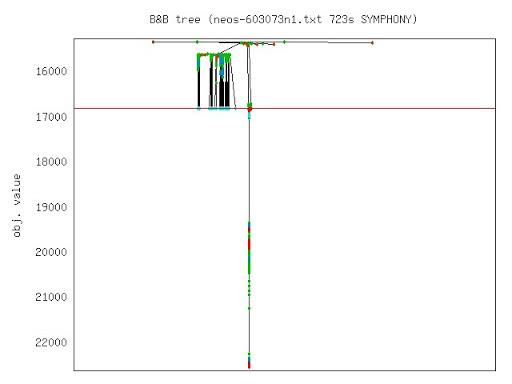
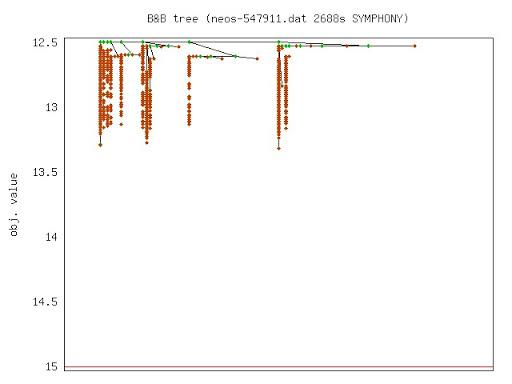
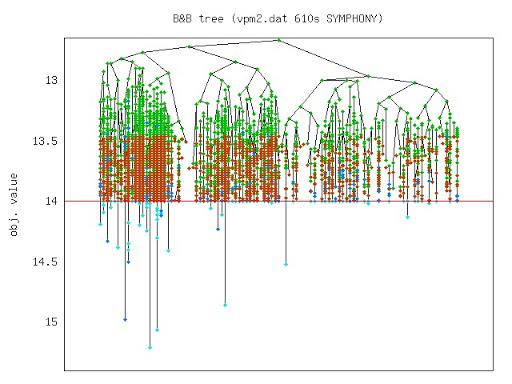
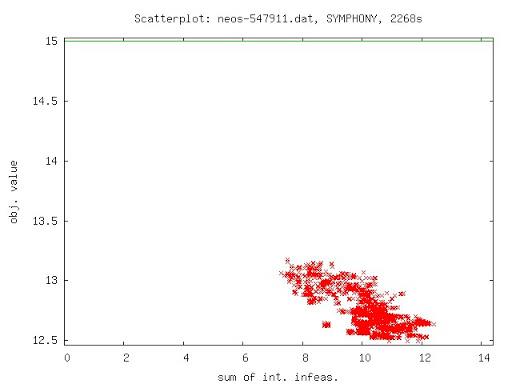
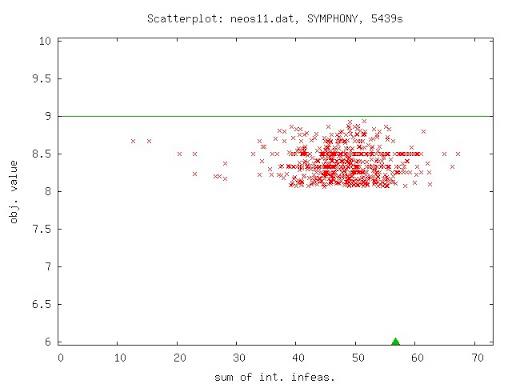
Short Course on Computational Integer Programming (Chinese Academy of Science)

These are the materials for a summer course given at the Academy of Mathematics and Systems Science of the Chinese Academy of Science as part of the 2016 International Workshop on Modern Optimization and Applications.
Lecture Slides
- Introduction
- Modeling and Formulation
- Software
- Python
- Algebraic Modeling: Part I
- Algebraic Modeling: Part II
- Linear Programming
- Branch and Bound
- Bounding
- Branching
- Cutting Plane Methods
- Branch and Cut
Sites with Additional Material
- Course on Linear Programming
- Course on Integer Programming
- Course on Computational Optimization
- Models
- Instance Gallery
Software
- Solver Suites
- Python
- Python Packages
- GiMPy (Documentation)
- GrUMPy (Documentation)
- CuPPy (Documentation)
- DIPPy
- xdot
- PyPolyhedron
- cyLP
- yaposib
- PuLP
- Pyomo
- Pygtk
- Other
Software Documentation
Instances
Reference Texts
- Integer Programming, M. Conforti, G. Cornuejols, and G. Zambelli, (2015).
- Constraint Integer Programming, T. Achterberg (2007).
- Integer and Combinatorial Optimization, G.L. Nemhauser and L.A. Wolsey, Wiley (1988).
- Integer Programming L.A. Wolsey, Wiley (1998).
- Theory of Linear and Integer Programming A. Schrijver, Wiley.
- Discrete Optimization R.G. Parker and R.L. Rardin, Academic Press.
- Optimization Over Integers, D. Bertsimas and R. Weismantel.
- Introduction to Linear Optimization, D. Bertsimas and J. Tsitsiklis.
- AMPL: A Modeling Language for Math Programming R. Fourer, D. M. Gay, B. W. Kernighan.
- Mathematics of Operations Research W.H. Marlow.
Additional Reading
- K. L. Hoffman and T. K. Ralphs (2011), Integer and Combinatorial Optimization.
- Some basic introductory articles on modeling tips and tricks
- Theory of Valid Inequalities
- R. Gomory (1958), Outline of an Algorithm for Integer Solutions to Linear Programs.
- G. Cornuejols (2006). Valid Inequalities for Mixed Integer Linear Programs.
- A. Saxena and E. Balas, Optimizing Over the Split Closure
- M. Perregaard, Generating Disjunctive Cuts for Mixed Integer Programs
- A. Caprara and A.N. Letchford, On the Separation of Split Cuts and Related Inequalities
- M. Conforti Corner Polyhedra and Intersection Cuts
- K. Aardal and C. van Hoesel(1996). Polyhedral Techniques in Combinatorial Optimization I: Theory. Statistica Neerlandica, 50:3-26, 1996.
- Z. Gu, G.L. Nemhauser, and M.W.P. Savelsbergh (2000). Sequence Independent Lifting. Journal of Combinatorial Optimization 4, 109-129.
- Preprocessing and Conflict Analysis
- A. Atamturk, G. Nemhauser, and M.W.P. Savelsburgh, Conflict Graphs in Solving Integer Programming Problems
- T. Achterburg Conflict Analysis in Mixed Integer Programming
- M.W.P. Savelsbergh (1994). Preprocessing and Probing for Mixed Integer Programming Problems. ORSA J. on Computing 6, 445-454.
- Reformulation and Decomposition
- F. Vanderbeck and L. Wolsey (2009). Reformulation and Decomposition of Integer Programs.
- T. Ralphs and M. Galati, Decomposition in Integer Programming, in Integer Programming: Theory and Practice, John Karlof, ed. (2005).
- D. Villeneuve, J. Desrosiers, M. Luebbecke, F. Soumis (2003). On Compact Formulations for Integer Programs Solved by Column Generation.
- L. Liberti (2008), Reformulations in Mathematical Programming: Symmetry.
- Branch and Cut
- M. W. Padberg and G. Rinaldi (1991). A branch-and-cut algorithm for the resolution of large-scale symmetric traveling salesman problems. SIAM Review 33, 60–100.
- A. Martin (2001), Computational Issues for Branch-and-Cut Algorithms. Computational Combinatorial Optimization, M. Juenger and D. Naddef, eds., 1-25.
- J.T. Linderoth and T.K. Ralphs (2005), Noncommercial Software for Mixed-Integer Linear Programming, in Integer Programming: Theory and Practice, John Karlof, ed. (2005), 253.
- W. Cook, R. Fukusawa, and G. Goycoolea, Choosing the Best Cuts
- K. Wolter Implementations of Cutting Plane Separators for Mixed Integer Programs
- K. Aardal and C. van Hoesel. Polyhedral Techniques in Combinatorial Optimization II: Applications and Computations. Statistica Neerlandica, 50:3-26, 1996.
- Branch and Price
- M. Luebbecke and J. Desrosier (2005). Selected Topics in Column Generation.
- C. Barnhart, E.L. Johnson, G.L. Nemhauser, M.W.P. Savelsbergh, P.H. Vance (1998). Branch-and-Price: Column Generation for Huge Integer Programs. Operations Research 46, 316-329.
- D.M. Ryan and B.A. Foster (1981). An Integer Programming Approach to Scheduling.
- Miscellaneous Computational Issues
- J.T. Linderoth and M.W.P. Savelsbergh (1999). Computational Study of Search Strategies for Mixed Integer Programming. INFORMS J. on Computing 11, 173-187.
- T. Acterburg, T. Koch, and A. Martin, Branching Rules Revisited. Operations Research Letters 33 (2005), 42-54.
- T. Berthold Primal Heuristics for Mixed Integer Programs
- F. Margot (2008), Symmetry in Integer Linear Programming.
- A. Martin (1999), Integer Programs with Block Structure.
- M. Karamanov and G. Cornuejols, Branching on General Disjunctions.
- K. Aardal, R. Weismantel, and L. Wolsey. Non-standard Approaches to Integer Programming. Discrete Applied Mathematics 123 (2002), 5-74.
- T. Koch, et al. (2011), MIPLIB 2010.
If you find something here useful, buy me a beer!