Lehigh ISE / COR@L Lab Wiki is our new system to create a collective information resource within the department.

From the Wikipedia ¹⁾ definition,

A wiki is a web application which allows people to add, modify, or delete content in collaboration with others. In a typical wiki, text is written using a simplified markup language (known as “wiki markup”) or a rich-text editor.

At this moment, Lehigh ISE / COR@L Lab Wiki is only open to faculty and PhD Student of Lehigh ISE department.

You can create new pages, edit the existing pages, upload resources or even delete the content from the system. You are free to share any information as long as it is in the interest of users.

First of all, you need to be registered to the system. Click here to register to the system.

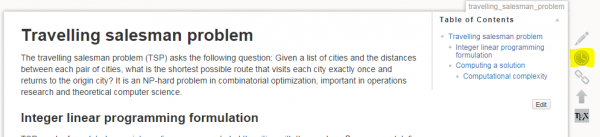
In a sample page, simply click the pen button on the right sidebar.

Then you will see the rich-text editor of the Dokuwiki.

Write the new address of the page you want, in the following format;

http://coral.ie.lehigh.edu/wiki/doku.php/new_page_name

Then click the same button that we used to edit pages, on the right sidebar. It will create the new page.

Delete all content of the page in the text editor and save.

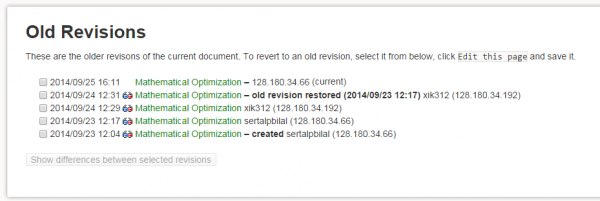
The wiki system has a revision control to restore old information to prevent loss of page content. Even if someone delete a page, you can click the revision button to reach the previous versions.

Wiki system can recognize mathematical formulations in tex format. The following input

$ \displaystyle x^2 + \sum_{i=1}^n y_i \leq \alpha $

gives

$ \displaystyle x^2 + \sum_{i=1}^n y_i \leq \alpha $

You can use \begin{equation} \end{equation} as well as \ref{label} type of LaTeX commands. For more information, check MathJax documentation.

You can export page content in TeX/LaTeX format. Click the TeX button on the right side for any page you want and compile it with your favorite editor. It can also export any image that are available in the page in a zip file. Check this sample output.

You can check the following sample pages and edit it without any registration.

• Travelling salesman problem
• Mathematical Optimization

If you want, you can watch the DokuWiki tutorials to learn more about the system.

For your questions, please reach one of the COR@L admins or INFORMS board members.