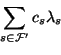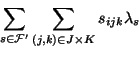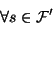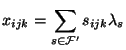

Next: Column Generation Algorithm
Up: Branch and Price for
Previous: Axial Assignment Problem
Balas and Saltzman [1] consider the use of the classical
Assignment Problem (AP) as a relaxation of AAP in the context of
Lagrangian Relaxation. We will use these same ideas in the context of
column generation or Dantzig-Wolfe decomposition.
Define the AP polytope by removing constraint (1)
as
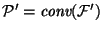 , where
, where
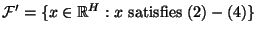 . Observe, that the cost of an assignment is
. Observe, that the cost of an assignment is
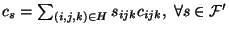 .
.
Then, the Dantzig Wolfe (DW) LP can be written as:
where
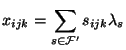 |
(8) |


Next: Column Generation Algorithm
Up: Branch and Price for
Previous: Axial Assignment Problem
IP Seminar Series
2003-12-01
![]() , where
, where
![]() . Observe, that the cost of an assignment is
. Observe, that the cost of an assignment is
![]() .
.