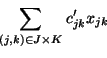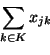

Next: BCP Implementation
Up: Branch and Price for
Previous: Dantzig-Wolfe Formulation
Since there is an exponential number of possible columns in the Dantzig-Wolfe
LP, we will use a column generation algorithm. Let
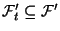 represent a subset of the feasible points in
represent a subset of the feasible points in
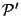 , i.e. assignment points. At iteration
, i.e. assignment points. At iteration 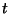 , the
restricted master problem is the Dantzig-Wolfe LP above with
, the
restricted master problem is the Dantzig-Wolfe LP above with
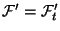 . Associate a vector of dual
variables
. Associate a vector of dual
variables 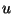 with constraint (4) and
with constraint (4) and 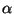 with
the convexity constraint (5). Let
with
the convexity constraint (5). Let
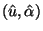 be the optimal dual solution to the restricted master problem. We then solve a
subproblem to search for the column from
be the optimal dual solution to the restricted master problem. We then solve a
subproblem to search for the column from
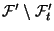 with the most negative reduced cost. The reduced cost of a variable
with the most negative reduced cost. The reduced cost of a variable
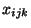 is calculated as
is calculated as
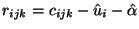 |
(9) |
Hence, we can write the column generation subproblem as an
optimization problem over the AP polytope as
where
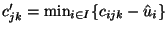 . Then, if
. Then, if
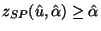 , then no columns in
, then no columns in
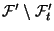 have
negative reduced cost and the solution to the restricted master is
optimal. Otherwise, we add the column
have
negative reduced cost and the solution to the restricted master is
optimal. Otherwise, we add the column 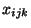 , corresponding to
the optimal solution of
, corresponding to
the optimal solution of
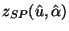 , to
, to
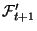 and iterate.
and iterate.


Next: BCP Implementation
Up: Branch and Price for
Previous: Dantzig-Wolfe Formulation
IP Seminar Series
2003-12-01