Axial Assignment Problem

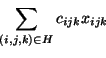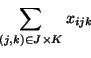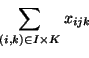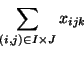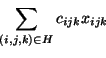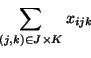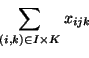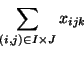
Next: Dantzig-Wolfe Formulation Up: Branch and Price for Previous: Branch and Price for

Axial Assignment Problem

The Axial Assignment Problem (AAP) is that of finding a minimum-weight clique cover of the complete tri-partite graph 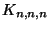$K_{n,n,n}$ . Let

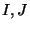and

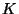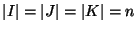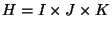be three disjoint sets with $\vert I\vert=\vert J\vert=\vert K\vert=n$ and set $H = I \times J \times K$ . Then, AAP can be formulated as the following binary integer program:

$\begin{displaymath} \min \end{displaymath}$ $\begin{displaymath}\sum_{(i,j,k) \in H} c_{ijk} x_{ijk} \nonumber \end{displaymath}$

$\begin{displaymath}\sum_{(j,k) \in J \times K} x_{ijk} \end{displaymath}$ $\begin{displaymath}= \end{displaymath}$ $\begin{displaymath}1 \end{displaymath}$ $\begin{displaymath}\forall i \in I \end{displaymath}$ (1)

$\begin{displaymath}\sum_{(i,k) \in I \times K} x_{ijk} \end{displaymath}$ $\begin{displaymath}= \end{displaymath}$ $\begin{displaymath}1 \end{displaymath}$ $\begin{displaymath}\forall j \in J \end{displaymath}$ (2)

$\begin{displaymath}\sum_{(i,j) \in I \times J} x_{ijk} \end{displaymath}$ $\begin{displaymath}= \end{displaymath}$ $\begin{displaymath}1 \end{displaymath}$ $\begin{displaymath}\forall k \in K \yesnumber \end{displaymath}$ (3)

$\begin{displaymath}x_{ijk} \in \{0,1\} \end{displaymath}$ $\begin{displaymath}\forall (i,j,k) \in H \end{displaymath}$ (4)

Next: Dantzig-Wolfe Formulation Up: Branch and Price for Previous: Branch and Price for

IP Seminar Series 2003-12-01

$\begin{displaymath} \min \end{displaymath}$	$\begin{displaymath}\sum_{(i,j,k) \in H} c_{ijk} x_{ijk} \nonumber \end{displaymath}$
	$\begin{displaymath}\sum_{(j,k) \in J \times K} x_{ijk} \end{displaymath}$	$\begin{displaymath}= \end{displaymath}$	$\begin{displaymath}1 \end{displaymath}$	$\begin{displaymath}\forall i \in I \end{displaymath}$	(1)
	$\begin{displaymath}\sum_{(i,k) \in I \times K} x_{ijk} \end{displaymath}$	$\begin{displaymath}= \end{displaymath}$	$\begin{displaymath}1 \end{displaymath}$	$\begin{displaymath}\forall j \in J \end{displaymath}$	(2)
	$\begin{displaymath}\sum_{(i,j) \in I \times J} x_{ijk} \end{displaymath}$	$\begin{displaymath}= \end{displaymath}$	$\begin{displaymath}1 \end{displaymath}$	$\begin{displaymath}\forall k \in K \yesnumber \end{displaymath}$	(3)
	$\begin{displaymath}x_{ijk} \in \{0,1\} \end{displaymath}$			$\begin{displaymath}\forall (i,j,k) \in H \end{displaymath}$	(4)