Deterministically Constrained Stochastic Optimization
This research thrust is considering the design, analysis, and implementation of algorithms for solving optimization problems with a stochastic objective function and deterministic constraints. Such problems are just now emerging in data science since large-scale decision-making applications demand the ability to solve problems with more realistic, nonlinear systems of equations/inequalities that impose constraints on the decision variables. Particular problem areas of interest to our group include the following:
- learning deep convolutional neural networks with smoothness properties imposed
- PDE-constrained inverse problems
- maximum likelihood estimation with constraints
- multi-stage modeling
- power engineering.
The figures to the right illustrate the performance of our method (Stochastic SQP) compared to the typically used stochastic subgradient method (Stochastic Subgradient). The box plots for feasibility error (top figure) and optimality error (bottom figure) created from our test problems show that our method consistently obtains better solution estimates in terms of feasibility and optimality over various noise levels for the stochastic objective functions.
This research is funded by the Office of Naval Research since 2021. My main collaborators are Albert Berahas, Frank E. Curtis, Minhan Li, Michael O’neill, and Baoyu Zhou.
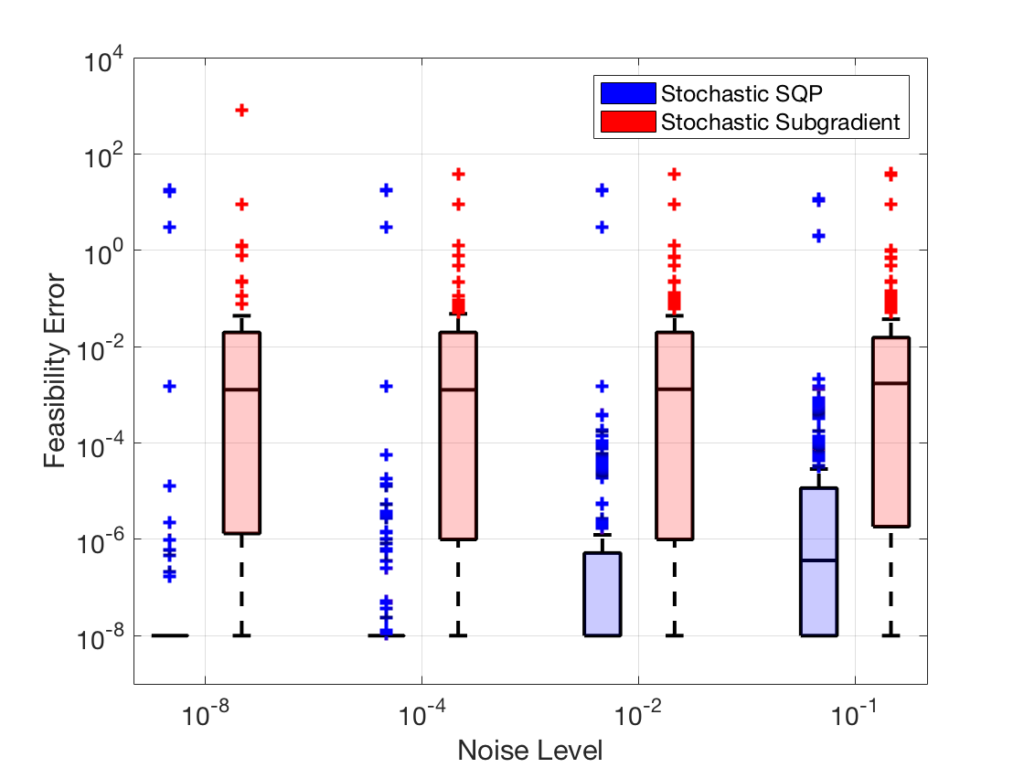
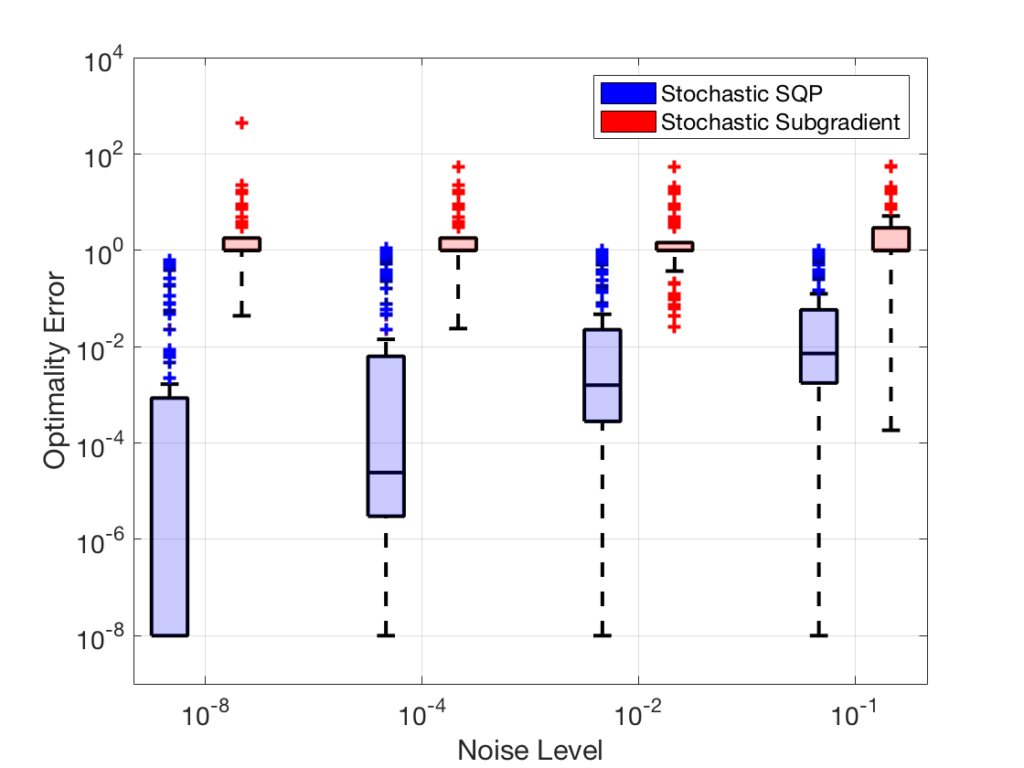
These figures are from the following publication: Albert Berahas, Frank E. Curtis, Daniel P. Robinson, and Baoyu Zhou. Sequential Quadratic Optimization for Nonlinear Equality Constrained Stochastic Optimization. arXiv preprint arXiv:2007.10525.

This figure can be found in the following publication: Tianyu Ding, Zhihui Zhu, Tianjiao Ding, Yunchen Yang, Rene Vidal, and Daniel P. Robinson. Noisy Dual Principal Component Pursuit. Proceedings of the 36th International Conference on Machine Learning, pages 1617-1625, 2019.
Subspace Clustering
We are designing and analyzing nonconvex optimization-based approaches for discovering high-dimensional structures in big and corrupted data. Examples include clustering high dimensional subspaces in 3D point clouds and unsupervised learning of object categories, which commonly appear in robotics and computer vision. We are currently focused on a Dual Principal Component Pursuit (DPCP) approach, which has routinely been shown to outperform other state-of-the-art algorithms.
The figure to the left illustrates a 3D point cloud analysis on frame 328 of the KITTY-CITY-71 data set, with inliers (blue) and outliers (red) indicated. The images demonstrate the projections of the 3D point cloud onto the image based on the subspace (the road) recovered by competing methods.
This research continues to be funded by the USA National Science Foundation under grant number NSF-1704458 since 2017. My main collaborators are Tianyu Ding, Manolis Tsakiris, Rene Vidal, and Zhihui Zhu.
Group-Sparse Regularization
This project considers the design and analysis of advanced algorithms for solving optimization problems that use group-sparsity inducing regularization. In some machine learning applications the covariates come in groups (e.g, genes that regulate hormone levels in microarray data), in which case one may wish to select them jointly. Standard one-norm regularization techniques fail to achieve this goal. Also, integrating group information into the modeling process can improve both the interpretability and accuracy of the models obtained.
The figure to the right illustrates the performance of our method (FaRSA-Group) compared to the state-of-the-art method gglasso. Each problem instance tested has a bar associated with it (a blue bar means that our method was more efficient and a red bar means gglasso was more efficient). One can see that our method FaRSA-Group significantly outperforms gglasso.
This research has been funded by the USA National Science Foundation under grant DMS-2012243 since 2020. My main collaborators are Frank E. Curtis and Yutong Dai.
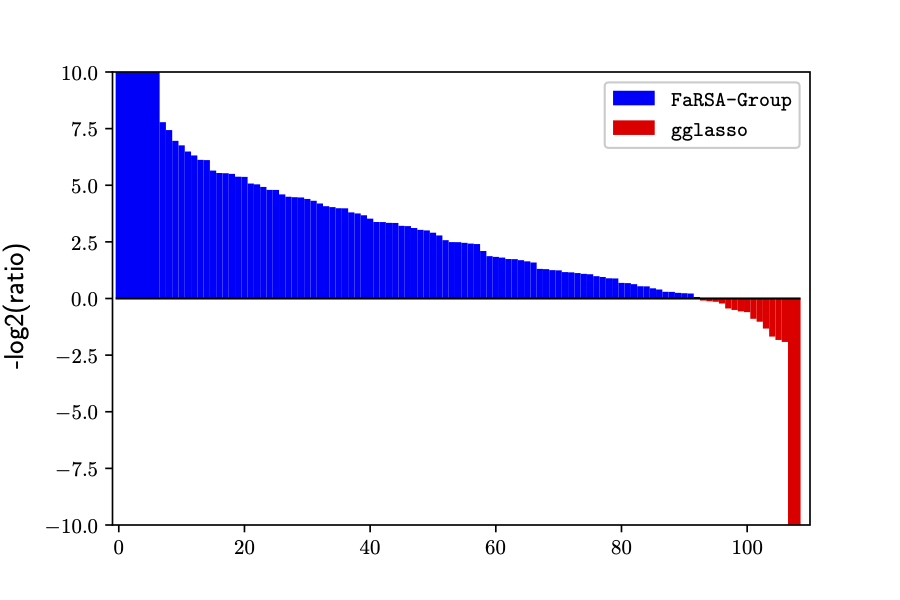
This figure can be found in the following publication: Frank E. Curtis, Yutong Dai, and Daniel P. Robinson. A Subspace Acceleration Method for Minimization Involving a Group Sparsity-Inducing Regularizer. arXiv preprint arXiv:2007.14951 (2020).
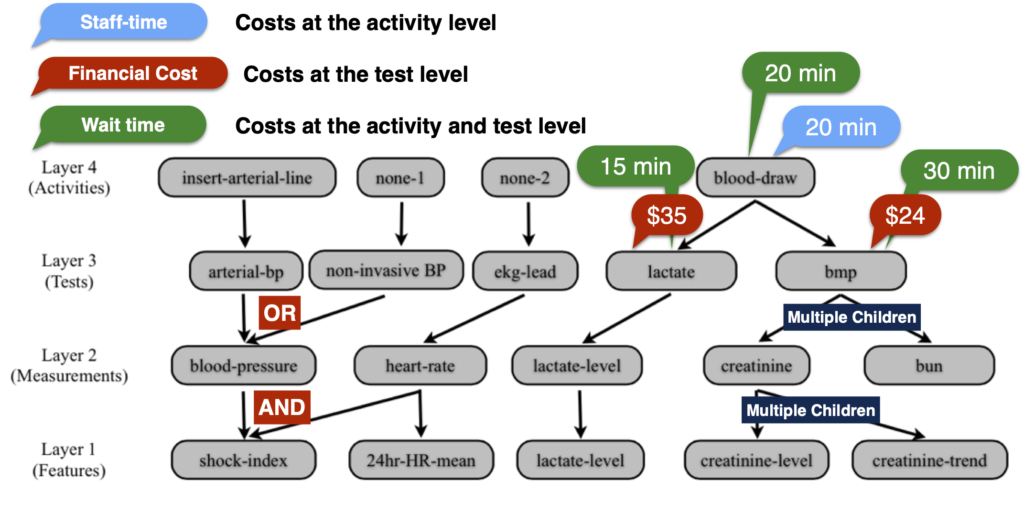
This cost structure graph can be found in the following publication: Suchi Saria and Daniel P. Robinson. Incorporating End-User Preferences in Predictive Models. International Joint Conferences on Artificial Intelligence, 2016.
Predicting Septic Shock
In many real-world applications, it is too restrictive to assume that the user can specify their cost preferences in terms of feature costs. We address this issue by designing a new regularizer that faithfully reflects the structure of the underlying cost graph. This regularizer may then be used to perform various prediction tasks via regularized risk minimization.
Consider the cost structure for deploying a predictive model in an Intensive Care Unit (ICU). A subset of measurements and tests used for ordering these measurements, along with their costs and dependencies, are shown in the illustration to the left. Since the cost structure is complicated, it is difficult to incorporate users’ preferences into the models that we seek. We have developed a new modeling framework to handle such challenges, and shown that it has improved the cost-predictive tradeoff compared to state-of-the-art methods in the task of predicting whether a patient will develop septic shock in an ICU setting.
